dialstatic
·Here's something that's been bugging me for a while now. We tend to check the accuracy of our watches on specific moments. What happens when we do a more longitudinal check of the accuracy, and plot the results over time?
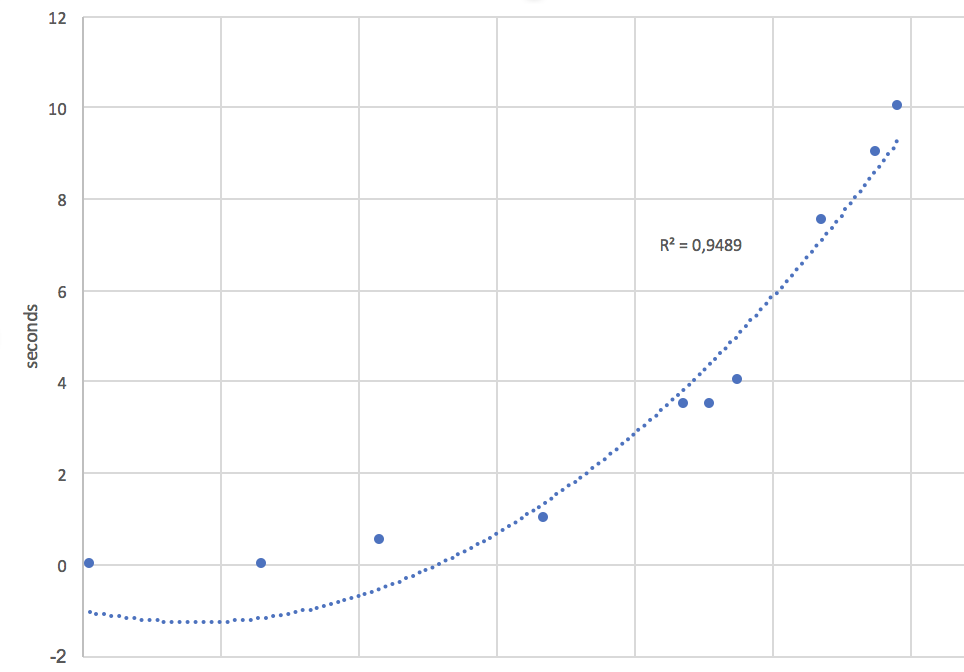
I've done this for two watches so far. One is a hand wound movement, the other an automatic (but I've left it just lying there until it runs out, so it's essentially a hand wound movement for purposes of my question). In both instances, I noticed that the deviation becomes larger as the hairspring uncoils. And it's not linear, either: it looks more or less like a second degree polynomial (see below for an example of a 30110 movement - an IWC modified 2892-A2).
Now my questions are:
1. Is it logical that the amount of time a watch gains (or loses) as it becomes more unwound, increases? In other words, is the accuracy a function of the degree to which a watch is wound?
2. Does is make mechanical sense that this should happen according to a quadratic equation?
I'd sure appreciate any responses, but just t be on the safe side, I'm tagging @Archer in this 😉
I've done this for two watches so far. One is a hand wound movement, the other an automatic (but I've left it just lying there until it runs out, so it's essentially a hand wound movement for purposes of my question). In both instances, I noticed that the deviation becomes larger as the hairspring uncoils. And it's not linear, either: it looks more or less like a second degree polynomial (see below for an example of a 30110 movement - an IWC modified 2892-A2).
Now my questions are:
1. Is it logical that the amount of time a watch gains (or loses) as it becomes more unwound, increases? In other words, is the accuracy a function of the degree to which a watch is wound?
2. Does is make mechanical sense that this should happen according to a quadratic equation?
I'd sure appreciate any responses, but just t be on the safe side, I'm tagging @Archer in this 😉
Edited: